A Recipient Uses Which of the Following to Read an Encrypted Message?

Cryptographic system with public and individual keys

An unpredictable (typically large and random) number is used to begin generation of an acceptable pair of keys suitable for employ by an disproportionate key algorithm.

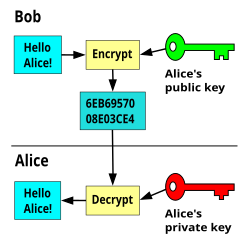
In an asymmetric cardinal encryption scheme, anyone tin encrypt messages using a public key, merely only the holder of the paired private key can decrypt such a bulletin. The security of the system depends on the secrecy of the private key, which must not become known to any other.

In the Diffie–Hellman fundamental exchange scheme, each political party generates a public/private key pair and distributes the public key of the pair. Afterward obtaining an accurate (n.b., this is disquisitional) re-create of each other's public keys, Alice and Bob tin compute a shared secret offline. The shared secret tin be used, for instance, equally the key for a symmetric goose egg which will be, in essentially all cases, much faster.

In this example the message is digitally signed, but not encrypted. 1) Alice signs a message with her private key. 2) Bob tin can verify that Alice sent the message and that the message has not been modified.

Public-key cryptography, or asymmetric cryptography, is a cryptographic system that uses pairs of keys. Each pair consists of a public cardinal (which may be known to others) and a private key (which may non be known by anyone except the owner).^[1] The generation of such key pairs depends on cryptographic algorithms which are based on mathematical problems termed one-way functions. Effective security requires keeping the private key private; the public central can be openly distributed without compromising security.^[2]

In such a organisation, whatever person can encrypt a message using the intended receiver's public key, but that encrypted message tin can only be decrypted with the receiver's private primal. This allows, for instance, a server plan to generate a cryptographic key intended for a suitable symmetric-key cryptography, so to utilize a client's openly-shared public key to encrypt that newly generated symmetric key. The server can then transport this encrypted symmetric fundamental over an insecure channel to the client; only the customer can decrypt it using the client'south private cardinal (which pairs with the public key used past the server to encrypt the message). With the client and server both having the same symmetric primal, they can safely use symmetric key encryption (likely much faster) to communicate over otherwise-insecure channels. This scheme has the reward of non having to manually pre-share symmetric keys (a fundamentally difficult problem) while gaining the higher data throughput advantage of symmetric-central cryptography.

With public-key cryptography, robust hallmark is besides possible. A sender can combine a bulletin with a individual key to create a short digital signature on the message. Anyone with the sender's corresponding public primal can combine that message with a claimed digital signature; if the signature matches the bulletin, the origin of the message is verified (i.e., it must have been made by the owner of the corresponding individual cardinal).^{[3] [4]}

Public key algorithms are primal security primitives in modernistic cryptosystems, including applications and protocols which offering balls of the confidentiality, authenticity and non-repudiability of electronic communications and information storage. They underpin numerous Internet standards, such every bit Transport Layer Security (TLS), Southward/MIME, PGP, and GPG. Some public primal algorithms provide key distribution and secrecy (e.grand., Diffie–Hellman fundamental substitution), some provide digital signatures (e.g., Digital Signature Algorithm), and some provide both (e.g., RSA). Compared to symmetric encryption, disproportionate encryption is rather slower than expert symmetric encryption, also slow for many purposes.^[5] Today's cryptosystems (such as TLS, Secure Shell) use both symmetric encryption and asymmetric encryption, often by using asymmetric encryption to deeply exchange a secret key which is so used for symmetric encryption.

Clarification [edit]

Before the mid-1970s, all zilch systems used symmetric cardinal algorithms, in which the same cryptographic cardinal is used with the underlying algorithm by both the sender and the recipient, who must both go along information technology hugger-mugger. Of necessity, the key in every such system had to exist exchanged between the communicating parties in some secure way prior to any utilise of the system – for instance, via a secure channel. This requirement is never picayune and very rapidly becomes unmanageable as the number of participants increases, or when secure channels aren't available, or when, (as is sensible cryptographic practise), keys are frequently changed. In particular, if messages are meant to be secure from other users, a carve up central is required for each possible pair of users.

By contrast, in a public central organization, the public keys can be disseminated widely and openly, and merely the corresponding private keys need be kept underground by its owner.

Two of the best-known uses of public key cryptography are:

• Public key encryption, in which a message is encrypted with the intended recipient'south public key. For properly chosen and used algorithms, letters cannot in practice be decrypted past anyone who does not possess the matching private key, who is thus presumed to be the possessor of that central and so the person associated with the public key. This tin be used to ensure confidentiality of a message.
• Digital signatures, in which a message is signed with the sender's private key and can be verified by anyone who has access to the sender's public key. This verification proves that the sender had admission to the private key, and therefore is very likely to be the person associated with the public key. This besides ensures that the message has not been tampered with, as a signature is mathematically bound to the message information technology originally was made from, and verification will fail for practically any other message, no thing how similar to the original bulletin.

1 important issue is confidence/proof that a particular public primal is accurate, i.e. that information technology is correct and belongs to the person or entity claimed, and has not been tampered with or replaced by some (perhaps malicious) third party. In that location are several possible approaches, including:

A public key infrastructure (PKI), in which one or more than third parties – known as certificate authorities – certify ownership of key pairs. TLS relies upon this. This implies that the PKI organization (software, hardware, and management) is trust-able by all involved.

A "spider web of trust" which decentralizes authentication by using individual endorsements of links between a user and the public key belonging to that user. PGP uses this approach, in add-on to lookup in the domain name arrangement (DNS). The DKIM system for digitally signing emails too uses this arroyo.

Applications [edit]

The virtually obvious application of a public key encryption system is for encrypting communication to provide confidentiality – a message that a sender encrypts using the recipient's public cardinal which tin be decrypted only by the recipient's paired private key.

Another application in public key cryptography is the digital signature. Digital signature schemes can be used for sender authentication.

Non-repudiation systems use digital signatures to ensure that one political party cannot successfully dispute its authorship of a document or communication.

Further applications built on this foundation include: digital cash, password-authenticated key agreement, fourth dimension-stamping services and not-repudiation protocols.

Hybrid Cryptosystems [edit]

Considering asymmetric cardinal algorithms are about always much more computationally intensive than symmetric ones, it is common to utilise a public/private disproportionate key-exchange algorithm to encrypt and exchange a symmetric key, which is so used by symmetric-central cryptography to transmit information using the now-shared symmetric key for a symmetric key encryption algorithm. PGP, SSH, and the SSL/TLS family of schemes use this procedure; they are thus called hybrid cryptosystems. The initial asymmetric cryptography-based primal exchange to share a server-generated symmetric key from the server to client has the advantage of non requiring that a symmetric key exist pre-shared manually, such every bit on printed paper or discs transported by a courier, while providing the college data throughput of symmetric key cryptography over disproportionate fundamental cryptography for the remainder of the shared connection.

Weaknesses [edit]

As with all security-related systems, information technology is important to identify potential weaknesses. Aside from poor choice of an asymmetric key algorithm (there are few which are widely regarded as satisfactory) or too short a key length, the master security risk is that the private primal of a pair becomes known. All security of messages, hallmark, etc., will and then be lost.

Algorithms [edit]

All public fundamental schemes are in theory susceptible to a "brute-force key search attack".^[6] All the same, such an attack is impractical if the amount of computation needed to succeed – termed the "piece of work factor" past Claude Shannon – is out of attain of all potential attackers. In many cases, the piece of work factor tin exist increased by simply choosing a longer primal. But other algorithms may inherently have much lower work factors, making resistance to a beast-force assail (e.g., from longer keys) irrelevant. Some special and specific algorithms have been developed to aid in attacking some public key encryption algorithms; both RSA and ElGamal encryption accept known attacks that are much faster than the brute-forcefulness arroyo.^[7] None of these are sufficiently improved to be really practical, however.

Major weaknesses have been plant for several formerly promising disproportionate central algorithms. The "knapsack packing" algorithm was plant to exist insecure after the evolution of a new attack.^[8] Equally with all cryptographic functions, public-key implementations may exist vulnerable to side-channel attacks that exploit information leakage to simplify the search for a secret fundamental. These are often independent of the algorithm being used. Enquiry is underway to both notice, and to protect against, new attacks.

Amending of public keys [edit]

Another potential security vulnerability in using disproportionate keys is the possibility of a "human-in-the-eye" assail, in which the communication of public keys is intercepted by a third party (the "human in the eye") and so modified to provide unlike public keys instead. Encrypted messages and responses must, in all instances, be intercepted, decrypted, and re-encrypted by the attacker using the correct public keys for the dissimilar advice segments so as to avoid suspicion.

A communication is said to exist insecure where information is transmitted in a mode that allows for interception (likewise chosen "sniffing"). These terms refer to reading the sender's private data in its entirety. A communication is particularly unsafe when interceptions can't exist prevented or monitored by the sender.^[9]

A human being-in-the-middle set on can be hard to implement due to the complexities of modern security protocols. However, the task becomes simpler when a sender is using insecure media such as public networks, the Internet, or wireless communication. In these cases an attacker can compromise the communications infrastructure rather than the information itself. A hypothetical malicious staff fellow member at an Internet service provider (ISP) might discover a man-in-the-eye attack relatively straightforward. Capturing the public key would only require searching for the fundamental equally it gets sent through the ISP's communications hardware; in properly implemented disproportionate key schemes, this is not a significant risk.

In some advanced human being-in-the-middle attacks, one side of the communication will see the original data while the other volition receive a malicious variant. Asymmetric man-in-the-centre attacks can prevent users from realizing their connection is compromised. This remains so even when one user's information is known to be compromised because the data appears fine to the other user. This can lead to confusing disagreements between users such as "it must be on your end!" when neither user is at mistake. Hence, man-in-the-middle attacks are only fully preventable when the communications infrastructure is physically controlled by one or both parties; such every bit via a wired route inside the sender's ain edifice. In summation, public keys are easier to alter when the communications hardware used by a sender is controlled by an attacker.^{[10] [11] [12]}

Public key infrastructure [edit]

One arroyo to prevent such attacks involves the utilize of a public key infrastructure (PKI); a fix of roles, policies, and procedures needed to create, manage, distribute, apply, store and revoke digital certificates and manage public-primal encryption. However, this has potential weaknesses.

For example, the certificate authority issuing the certificate must be trusted by all participating parties to accept properly checked the identity of the primal-holder, to have ensured the correctness of the public key when it issues a certificate, to be secure from reckoner piracy, and to have made arrangements with all participants to check all their certificates earlier protected communications tin brainstorm. Web browsers, for instance, are supplied with a long list of "self-signed identity certificates" from PKI providers – these are used to check the bona fides of the certificate authority and then, in a 2nd step, the certificates of potential communicators. An aggressor who could subvert one of those certificate authorities into issuing a certificate for a bogus public fundamental could then mount a "man-in-the-center" attack as easily as if the document scheme were not used at all. In an alternative scenario rarely discussed,^{[ citation needed ]} an attacker who penetrates an authorisation's servers and obtains its store of certificates and keys (public and private) would exist able to spoof, masquerade, decrypt, and forge transactions without limit.

Despite its theoretical and potential problems, this approach is widely used. Examples include TLS and its predecessor SSL, which are ordinarily used to provide security for web browser transactions (for example, to securely send credit bill of fare details to an online store).

Aside from the resistance to attack of a particular key pair, the security of the certification bureaucracy must be considered when deploying public fundamental systems. Some certificate authorisation – commonly a purpose-built program running on a server computer – vouches for the identities assigned to specific individual keys by producing a digital certificate. Public key digital certificates are typically valid for several years at a fourth dimension, so the associated private keys must exist held deeply over that time. When a private key used for certificate creation college in the PKI server hierarchy is compromised, or accidentally disclosed, then a "man-in-the-center attack" is possible, making whatever subordinate certificate wholly insecure.

Examples [edit]

Examples of well-regarded asymmetric key techniques for varied purposes include:

• Diffie–Hellman fundamental exchange protocol
• DSS (Digital Signature Standard), which incorporates the Digital Signature Algorithm
• ElGamal
• Elliptic-curve cryptography
  • Elliptic Curve Digital Signature Algorithm (ECDSA)
  • Elliptic-curve Diffie–Hellman (ECDH)
  • Ed25519 and Ed448 (EdDSA)
  • X25519 and X448 (ECDH/EdDH)
• Diverse password-authenticated key agreement techniques
• Paillier cryptosystem
• RSA encryption algorithm (PKCS#1)
• Cramer–Shoup cryptosystem
• YAK authenticated key agreement protocol

Examples of asymmetric key algorithms not yet widely adopted include:

• NTRUEncrypt cryptosystem
• McEliece cryptosystem

Examples of notable – however insecure – asymmetric key algorithms include:

• Merkle–Hellman knapsack cryptosystem

Examples of protocols using asymmetric cardinal algorithms include:

• Southward/MIME
• GPG, an implementation of OpenPGP, and an Cyberspace Standard
• EMV, EMV Certificate Say-so
• IPsec
• PGP
• ZRTP, a secure VoIP protocol
• Ship Layer Security standardized by IETF and its predecessor Secure Socket Layer
• SILC
• SSH
• Bitcoin
• Off-the-Record Messaging

History [edit]

During the early history of cryptography, two parties would rely upon a key that they would substitution by means of a secure, merely not-cryptographic, method such as a face-to-face meeting, or a trusted courier. This key, which both parties must then keep absolutely secret, could then exist used to exchange encrypted messages. A number of significant applied difficulties arise with this approach to distributing keys.

Anticipation [edit]

In his 1874 volume The Principles of Scientific discipline, William Stanley Jevons^[13] wrote:

Can the reader say what 2 numbers multiplied together will produce the number 8616460799?^[14] I think it unlikely that anyone simply myself volition e'er know.^[fifteen]

Here he described the relationship of one-way functions to cryptography, and went on to talk over specifically the factorization trouble used to create a trapdoor function. In July 1996, mathematician Solomon Westward. Golomb said: "Jevons anticipated a cardinal feature of the RSA Algorithm for public key cryptography, although he certainly did not invent the concept of public key cryptography."^[xvi]

Classified discovery [edit]

In 1970, James H. Ellis, a British cryptographer at the United kingdom Government Communications Headquarters (GCHQ), conceived of the possibility of "non-secret encryption", (now called public central cryptography), only could run across no way to implement it.^{[17] [xviii]} In 1973, his colleague Clifford Cocks implemented what has get known as the RSA encryption algorithm, giving a practical method of "non-cloak-and-dagger encryption", and in 1974 some other GCHQ mathematician and cryptographer, Malcolm J. Williamson, developed what is at present known equally Diffie–Hellman key exchange. The scheme was also passed to the USA's National Security Agency.^[19] Both organisations had a military focus and only limited computing power was available in whatever instance; the potential of public key cryptography remained unrealised by either system:

I judged it most of import for armed forces use ... if you can share your key rapidly and electronically, you take a major advantage over your opponent. Just at the end of the evolution from Berners-Lee designing an open internet architecture for CERN, its adaptation and adoption for the Arpanet ... did public central cryptography realise its full potential.

—Ralph Benjamin^[19]

These discoveries were not publicly acknowledged for 27 years, until the research was declassified past the British government in 1997.^[20]

Public discovery [edit]

In 1976, an asymmetric key cryptosystem was published by Whitfield Diffie and Martin Hellman who, influenced by Ralph Merkle'due south work on public key distribution, disclosed a method of public key agreement. This method of key substitution, which uses exponentiation in a finite field, came to be known equally Diffie–Hellman key substitution.^[21] This was the offset published practical method for establishing a shared secret-fundamental over an authenticated (only non confidential) communications channel without using a prior shared cloak-and-dagger. Merkle'south "public key-agreement technique" became known as Merkle'due south Puzzles, and was invented in 1974 and only published in 1978.

In 1977, a generalization of Cocks' scheme was independently invented by Ron Rivest, Adi Shamir and Leonard Adleman, all then at MIT. The latter authors published their work in 1978 in Martin Gardner's Scientific American column, and the algorithm came to be known equally RSA, from their initials.^[22] RSA uses exponentiation modulo a product of 2 very big primes, to encrypt and decrypt, performing both public key encryption and public key digital signatures. Its security is connected to the extreme difficulty of factoring large integers, a problem for which in that location is no known efficient general technique (though prime number factorization may be obtained through creature-force attacks; this grows much more hard the larger the prime factors are). A description of the algorithm was published in the Mathematical Games column in the August 1977 issue of Scientific American.^[23]

Since the 1970s, a large number and variety of encryption, digital signature, key agreement, and other techniques take been developed, including the Rabin cryptosystem, ElGamal encryption, DSA - and elliptic curve cryptography.

See besides [edit]

• Books on cryptography
• GNU Privacy Guard
• ID-based encryption (IBE)
• Cardinal escrow
• Key-understanding protocol
• PGP word list
• Post-quantum cryptography
• Pretty Good Privacy
• Pseudonymity
• Public key fingerprint
• Public key infrastructure (PKI)
• Quantum computing
• Breakthrough cryptography
• Secure Beat (SSH)
• Symmetric-key algorithm
• Threshold cryptosystem
• Web of trust

Notes [edit]

1. ^ R. Shirey (Baronial 2007). Cyberspace Security Glossary, Version 2. Network Working Group. doi:10.17487/RFC4949. RFC 4949.
2. ^ Stallings, William (three May 1990). Cryptography and Network Security: Principles and Practice. Prentice Hall. p. 165. ISBN9780138690175.
3. ^ Menezes, Alfred J.; Oorschot, Paul C. van; Vanstone, Scott A. (Oct 1996). "11: Digital Signatures" (PDF). Handbook of Applied Cryptography. CRC Printing. ISBN0-8493-8523-7 . Retrieved xiv Nov 2016.
4. ^ Bernstein, Daniel J. (i May 2008). "Protecting communications confronting forgery" (PDF). Algorithmic Number Theory. Vol. 44. MSRI Publications. §5: Public-fundamental signatures, pp. 543–545. Retrieved 14 November 2016.
5. ^ Alvarez, Rafael; Caballero-Gil, Cándido; Santonja, Juan; Zamora, Antonio (27 June 2017). "Algorithms for Lightweight Key Substitution". Sensors. 17 (7): 1517. doi:10.3390/s17071517. ISSN 1424-8220. PMC5551094. PMID 28654006.
6. ^ Paar, Christof; Pelzl, January; Preneel, Bart (2010). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. ISBN978-3-642-04100-6.
7. ^ Mavroeidis, Vasileios, and Kamer Vishi, "The Impact of Quantum Computing on Present Cryptography", International Periodical of Avant-garde Computer Science and Applications, 31 March 2018
8. ^ Shamir, Adi (Nov 1982). "A polynomial time algorithm for breaking the bones Merkle-Hellman cryptosystem". 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982): 145–152. doi:ten.1109/SFCS.1982.five.
9. ^ Tunggal, Abi (20 February 2020). "What Is a Man-in-the-Middle Attack and How Can It Be Prevented - What is the difference betwixt a human-in-the-middle assault and sniffing?". UpGuard . Retrieved 26 June 2020.
10. ^ Tunggal, Abi (20 February 2020). "What Is a Man-in-the-Centre Assault and How Can Information technology Be Prevented - Where exercise man-in-the-middle attacks happen?". UpGuard . Retrieved 26 June 2020.
11. ^ martin (30 January 2013). "China, GitHub and the man-in-the-center". GreatFire. Archived from the original on 19 Baronial 2016. Retrieved 27 June 2015.
12. ^ percy (4 September 2014). "Authorities launch man-in-the-heart attack on Google". GreatFire . Retrieved 26 June 2020.
13. ^ Jevons, William Stanley, The Principles of Scientific discipline: A Treatise on Logic and Scientific Method p. 141, Macmillan & Co., London, 1874, 2nd ed. 1877, 3rd ed. 1879. Reprinted with a foreword past Ernst Nagel, Dover Publications, New York, NY, 1958.
14. ^ This came to be known as "Jevons'southward number". The only nontrivial cistron pair is 89681 × 96079.
15. ^ Principles of Science, Macmillan & Co., 1874, p. 141.
16. ^ Golob, Solomon W. (1996). "On Factoring Jevons' Number". Cryptologia. 20 (3): 243. doi:10.1080/0161-119691884933. S2CID 205488749.
17. ^ Ellis, James H. (January 1970). "THE POSSIBILITY OF SECURE Non-Undercover DIGITAL ENCRYPTION" (PDF).
18. ^ Sawer, Patrick (11 March 2016). "The unsung genius who secured Britain's reckoner defences and paved the way for prophylactic online shopping". The Telegraph.
19. ^ ^{a b} Espiner, Tom (26 Oct 2010). "GCHQ pioneers on birth of public key crypto". www.zdnet.com.
20. ^ Singh, Simon (1999). The Lawmaking Book. Doubleday. pp. 279–292.
21. ^ Diffie, Whitfield; Hellman, Martin East. (November 1976). "New Directions in Cryptography" (PDF). IEEE Transactions on Data Theory. 22 (6): 644–654. CiteSeerX10.1.1.37.9720. doi:ten.1109/TIT.1976.1055638. Archived (PDF) from the original on 29 November 2014.
22. ^ Rivest, R.; Shamir, A.; Adleman, Fifty. (February 1978). "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems" (PDF). Communications of the ACM. 21 (2): 120–126. CiteSeerXx.1.1.607.2677. doi:ten.1145/359340.359342. S2CID 2873616.
23. ^ Robinson, Sara (June 2003). "Withal Guarding Secrets later on Years of Attacks, RSA Earns Accolades for its Founders" (PDF). SIAM News. 36 (v).

References [edit]

• Hirsch, Frederick J. "SSL/TLS Stiff Encryption: An Introduction". Apache HTTP Server . Retrieved 17 April 2013. {{cite web}}: CS1 maint: url-status (link). The showtime two sections incorporate a very good introduction to public-cardinal cryptography.
• Ferguson, Niels; Schneier, Bruce (2003). Practical Cryptography. Wiley. ISBN0-471-22357-3.
• Katz, Jon; Lindell, Y. (2007). Introduction to Modern Cryptography. CRC Press. ISBN978-1-58488-551-1.
• Menezes, A. J.; van Oorschot, P. C.; Vanstone, Scott A. (1997). Handbook of Applied Cryptography. ISBN0-8493-8523-7.
• IEEE 1363: Standard Specifications for Public-Central Cryptography
• Christof Paar, Jan Pelzl, "Introduction to Public-Primal Cryptography", Chapter six of "Agreement Cryptography, A Textbook for Students and Practitioners". (companion web site contains online cryptography course that covers public-fundamental cryptography), Springer, 2009.

• Salomaa, Arto (1996). Public-Fundamental Cryptography (2 ed.). Berlin: Springer. 275. doi:10.1007/978-3-662-03269-5. ISBN978-three-662-03269-5. S2CID 24751345.

External links [edit]

• Oral history interview with Martin Hellman, Charles Babbage Institute, University of Minnesota. Leading cryptography scholar Martin Hellman discusses the circumstances and primal insights of his invention of public key cryptography with collaborators Whitfield Diffie and Ralph Merkle at Stanford University in the mid-1970s.
• An account of how GCHQ kept their invention of PKE hole-and-corner until 1997

montoyathationeath.blogspot.com

Source: https://en.wikipedia.org/wiki/Public-key_cryptography

Share this post